Scary Triangles - 恐ろしい三角形
Scary Triangles(恐ろしい三角形)
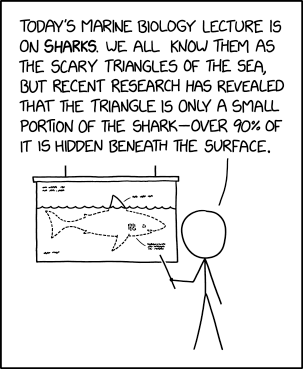
男: Today's marine biology lecture is on sharks. We all know them as the scary triangles of the sea, but recent research has revealed that the triangle is only a small portion of the shark - over 90% of it is hidden beneath the surface.
(今日の海洋生物学の講義はサメについて。僕らは皆、サメを海の怖い三角形として知っているが、最近の研究で、三角形はサメのほんの一部で、90%以上は水面下に隠れていることが明らかになった。)ALt-text: Concealed mostly beneath the surface, sharks are the icebergs of the sea.
(ほとんど水面下に隠れているサメは、海の氷山である。)
補足
恐ろしい三角形は実はサメだった!!!
XKCDカテゴリの記事について
- この記事は、世界で人気のWebコミック「xkcd」の最新コミックを日本語に翻訳しています。
- 過去の記事はxkcd日本語訳(2023年)、xkcd日本語訳(2022年)、過去の記事はxkcd日本語訳(2021年)、xkcd日本語訳(2020年)、xkcd日本語訳(2019年)、xkcd日本語訳(2018年)、xkcd日本語訳(2017年)、xkcd日本語訳(2016年)、xkcd日本語訳(2015年)、xkcd日本語訳(2014年)、xkcd日本語訳(2013年)、xkcd日本語訳からどうぞ。
- 秀逸なコミックは、過去のランキングベスト10の記事、2009年から2010年、2011年、2012年、2013年、2014年、2015年でまとめています。
- なお、英文が難解な場合は、クオリティの低い訳文をUPしてしまうことも多々ありますが、自ら気づいたり、皆様からの指摘があれば、正しい訳文にその都度直していきます。もし誤訳を見つけましたら、コメントなどで気軽にご指摘下さい。